El plano cartesiano es una herramienta fundamental en matemáticas que permite representar gráficamente puntos, líneas y figuras en dos dimensiones. Aunque su uso puede parecer técnico al principio, en realidad está presente en numerosos aspectos de la vida cotidiana, desde mapas hasta gráficas económicas o diseño técnico. Por ello, entender qué es y cómo funciona resulta esencial para estudiantes, profesionales y cualquier persona interesada en el razonamiento lógico o visual.
A continuación, exploraremos su origen, estructura y aplicaciones, de forma clara y accesible.
¿Cuál es el origen del plano cartesiano?
El plano cartesiano fue desarrollado por el filósofo y matemático René Descartes en el siglo XVII. Su idea consistía en unir el álgebra con la geometría para facilitar la representación de ecuaciones a través de gráficas. Esta combinación revolucionó el pensamiento matemático de su época y sentó las bases para el desarrollo del cálculo y otras ramas más avanzadas.
Gracias a esta invención, es posible resolver problemas espaciales de forma numérica y visual. Además, abrió el camino para que las matemáticas se conectaran con otras ciencias, como la física, la economía y la informática.
Componentes principales del plano cartesiano
El eje horizontal y el eje vertical
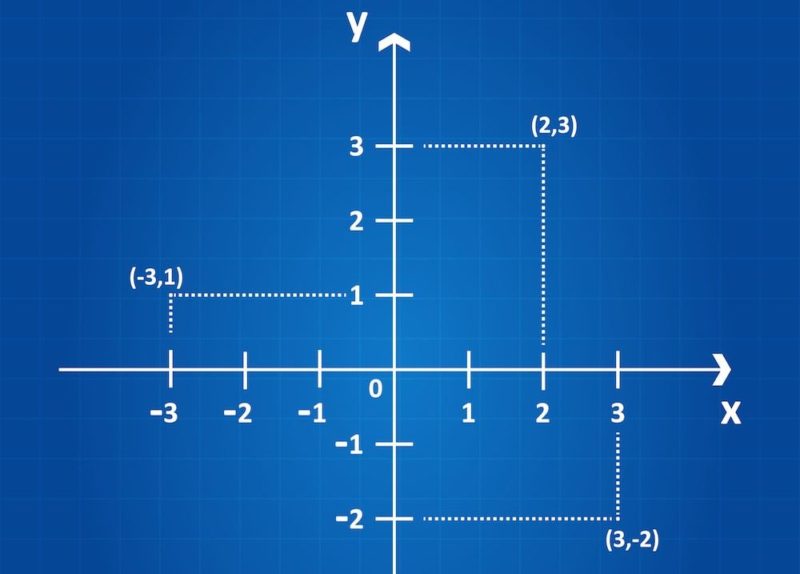
El plano cartesiano se compone de dos líneas numéricas que se cruzan en ángulo recto. La línea horizontal se conoce como eje X, mientras que la vertical se llama eje Y. El punto donde ambos ejes se cruzan es el origen, que tiene coordenadas (0, 0).
Este sistema permite localizar cualquier punto mediante un par ordenado de números. Por ejemplo, el punto (3, -2) indica que desde el origen se debe avanzar tres unidades a la derecha y dos hacia abajo.
Cuadrantes del plano
Al dividirse por los ejes X e Y, el plano cartesiano se organiza en cuatro regiones llamadas cuadrantes. Cada uno tiene combinaciones distintas de signos:
-
Primer cuadrante: (+, +)
-
Segundo cuadrante: (−, +)
-
Tercer cuadrante: (−, −)
-
Cuarto cuadrante: (+, −)
Por tanto, conocer en qué cuadrante se encuentra un punto ayuda a interpretar su ubicación relativa. Además, este conocimiento es clave al graficar funciones o figuras geométricas.

¿Cómo se representan los puntos en el plano cartesiano?
Para ubicar un punto, se utiliza un par ordenado (x, y). El primer número representa la posición horizontal (eje X) y el segundo, la posición vertical (eje Y). Aunque parezca complejo al principio, con la práctica este sistema se vuelve intuitivo.
Por ejemplo:
-
El punto (4, 2) se ubica 4 unidades a la derecha y 2 hacia arriba.
-
El punto (−3, −1) se localiza 3 unidades a la izquierda y 1 hacia abajo.
Además, los puntos pueden unirse con líneas para formar figuras, representar trayectorias o visualizar relaciones matemáticas.
Aplicaciones prácticas del plano cartesiano
En la educación y el aprendizaje
Uno de los usos más comunes del plano cartesiano es en el ámbito educativo. Se enseña desde niveles básicos, ya que ayuda a desarrollar habilidades espaciales, de análisis y lógica. Por ejemplo, los estudiantes aprenden a graficar funciones lineales o parabólicas, lo que facilita la comprensión de relaciones algebraicas.
Además, este conocimiento sirve como base para materias más complejas como trigonometría, geometría analítica y cálculo.
En el mundo real
Aunque pueda parecer lejano a la vida diaria, el plano cartesiano se aplica constantemente. Por ejemplo:
-
En la ingeniería, se usa para diseñar estructuras y calcular distancias entre puntos.
-
En economía, sirve para graficar la relación entre oferta y demanda.
-
En informática, es esencial para crear gráficos y videojuegos en dos dimensiones.
-
En la medicina, se utiliza para representar datos estadísticos o imágenes radiográficas digitalizadas.
Como puedes ver, sus usos van mucho más allá del aula.
¿Qué ventajas ofrece el uso del plano cartesiano?
El plano cartesiano permite representar de forma clara y precisa conceptos abstractos. Además, favorece el análisis visual, lo que ayuda a detectar patrones, tendencias o relaciones entre variables. Este enfoque visual resulta especialmente útil cuando los números por sí solos no bastan para entender una situación.
Por otro lado, al usar coordenadas, se pueden hacer cálculos más exactos y confiables. Esto es crucial en áreas como la arquitectura, donde un error mínimo podría generar problemas graves.
Errores comunes al trabajar con el plano cartesiano
Aunque el sistema es lógico, existen errores frecuentes, especialmente al comenzar a usarlo. Algunos de los más comunes incluyen:
-
Confundir el orden de las coordenadas (poner Y antes que X).
-
Ubicar puntos en el cuadrante incorrecto.
-
No considerar los signos negativos correctamente.
-
Leer el eje vertical como si fuera horizontal, y viceversa.
Sin embargo, estos errores disminuyen con la práctica y el uso continuo del plano.
Conclusión
En resumen, el plano cartesiano es una herramienta matemática poderosa que permite representar puntos, líneas y funciones en dos dimensiones. Su estructura simple pero eficaz facilita la resolución de problemas y la visualización de conceptos abstractos. Además, tiene múltiples aplicaciones prácticas en distintas áreas del conocimiento y la vida cotidiana.
Por tanto, aprender a utilizarlo correctamente es una habilidad esencial que aporta claridad, precisión y lógica a nuestras ideas. Ya sea en el aula, en una oficina o incluso en un videojuego, el plano cartesiano está más presente de lo que imaginamos. Entenderlo no solo mejora nuestras competencias matemáticas, sino que también nos prepara para enfrentar desafíos con un enfoque analítico y visual.